Reversible computers

Reversible computers

Welcome to the WWW page of the

reversible computer

at the Universiteit Gent



NEWS FLASH: NEW BOOK


In August 2018, publisher Morgan & Claypool published a brand new book:
"Synthesis of quantum circuits versus synthesis of classical reversible circuits"


by Alexis De Vos, Stijn De Baerdemacker, and Yvan Van Rentergem:




NEWS FLASH: RC 2022 CONFERENCE


After the successful international workshops/conferences on reversible computation, i.e.
RC2009, on 22 March 2009, in York,
RC2010, on 2-3 July 2010, in Bremen,
RC2011, on 4-5 July 2011, in Gent
RC2012, on 2-3 July 2012, in København,
RC2013, on 4-5 July 2013, in Victoria,
RC2014, on 10-11 July 2014, in Kyoto,
RC2015, on 16-17 July 2015, in Grenoble,
RC2016, on 7-8 July 2016, in Bologna,
RC2017, on 6-7 July 2017, in Kolkata,
RC2018, on 12-14 September 2018, in Leicester,
RC2019, on 24-25 June 2019, in Lausanne,
RC2020, on 9-10 July 2020, in Oslo, and
RC2021, on 7-8 July 2021, in Nagoya,
the fourteenth event, i.e. RC2022, will take place in Urbino, in July 2022.


Reversible computers are computers that can calculate both forwards and backwards:

They are based on reversible logic operations. For an introduction: see the two text books above. One can also read an early book on the subject: Addison Wesley (1996) published `Feynman lectures on computation', containing an excellent tutorial introduction to the subject.

At the Universiteit Gent we design, fabricate and test basic building blocks for such computers. They are based on the theoretical work by the Fredkin--Toffoli group of Massachusetts Institute of Technology. The design and fabrication happens in close collaboration with the Invomec division of Imec v.z.w. in Leuven.

We use standard c-MOS technology, but full-custom design. The processing of the chips happens within the Europractice consortium. Here is a reversible logic gate with three logic inputs and three logic outputs, seen through an optical microscope:

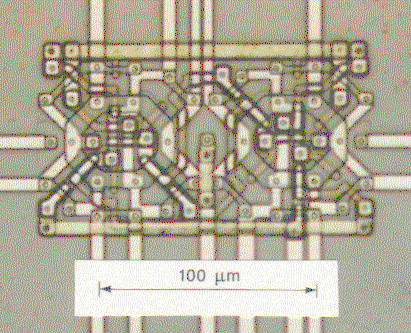
A scanning electron microscope gives more depth and perspective :

The circuit consists of 24 transistors (twelve n-MOS and twelve p-MOS), arranged on the edges of two hexagons. Particular is the fact that the circuit works without help of any power suppies (no V_dd nor V_ss nor ground busbars). All energy provided to the output pins, comes from the input pins.

More complex circuits, containing e.g. six such building blocks, have been realised successfully. Here is one of them: because it contains exactly 144 transistors, we call it our `gross' circuit:

The following four-bit ripple adder makes use of sixteen building blocks and thus contains 384 transistors :

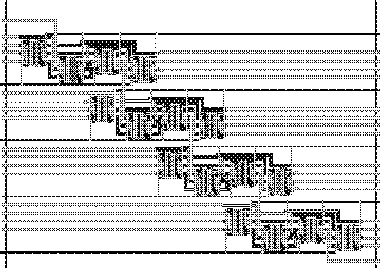
Many different 4-bit reversible adders have been designed. The second ripple adder uses Feynman's three building blocks: the NOT, the CONTROLLED NOT, and the CONTROLLED CONTROLLED NOT. It needs only 192 transistors, but performs equally well. The carry-look-ahead adder needs more transistors (i.e. 320), but is faster. It uses a generalization of the Feynman gates, i.e. the so-called control gates. Here it is:

In a control gate, one bit is inverted, on condition that some boolean function of some other bits equals one. Besides such controlled NOT gates, a.k.a. Toffoli gates, we also use controlled SWAP gates, a.k.a. Fredkin gates.

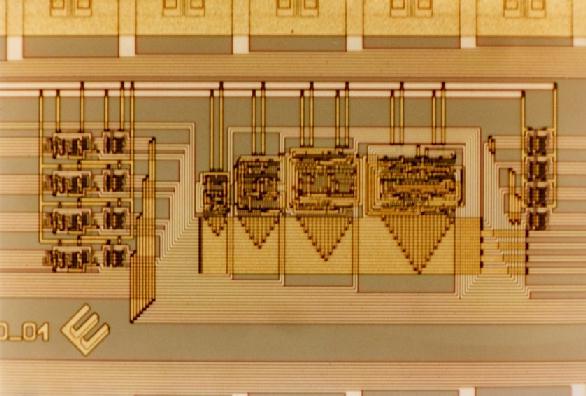
Here is an ambitious project: this chip contains 2,504 transistors. It reversibly multiplies an arbitrary 8-bit number with the number sqrt(2)/2.

It contains four adders and four subtracters. The adders (and subtracters) are of the ingeneous reversible type called the Cuccaro addition circuit (2005). Here is one of the four 8-bit Cuccaro adders (140 micrometer * 230 micrometer):

These reversible c-MOS techniques, we call reversible MOS or `r-MOS'. They are particularly suited for so-called adiabatic switching. Here is an experimental oscilloscope picture, showing an adiabatic input signal A_0 and a resulting output signal C_4 of an adder circuit.

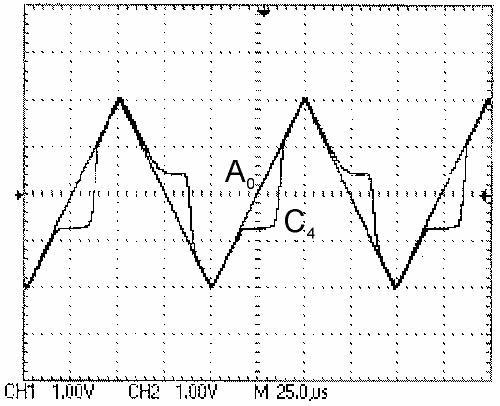
Unfortunately signal C_4 does not follow signal A_0 well in the range +/- 1 volt. This is caused by the threshold voltages of the transistors (about 0.8 volts here). Nevertheless, adiabatic adressing can save one order of magnitude in the power dissipation.

For more information on reversible computing techniques:

Research staff involved in Gent consists of:

Former research staff involved consists of:

For the mathematical aspects (group theory), there is close collaboration with the department of mathematics, more precisely with and with the department of physics and astronomy, more precisely with now at the chemistry department of the University of New Brunswick, Canada.

The project has been sponsored by the special research fund Bijzonder Onderzoeksfonds under the following grants:

by the Fonds Wetenschappelijk Onderzoek Vlaanderen, the science foundation of the Flemish government: by the " Commission on Strategic Growth Technologies (strategiske vaekstteknologier) " of the Danish ministry for research, technology and innovation: and by the European COST Association: The following photographs illustrate the close research collaboration with the informatics department of the Copenhagen University (Danmark):


 



Dr. Burignat (Gent) and Dr. Thomsen (København) are measuring the cascade of a do and an undo chip, thus illustrating the reversibility of the circuit.




MAIN REFERENCES :

Reference # 1 : a beautiful circuit
B. Desoete and A. De Vos published a paper entitled `` A reversible carry-look-ahead adder using control gates '', in Integration, the V.L.S.I. Journal, volume 33 (2002) pp. 89-104.

Reference # 2 : a beautiful theorem from group theory
A. De Vos and L. Storme published a paper entitled `` r-Universal reversible logic gates '', in Journal of Physics A: Mathematical and General, volume 37 (2004) pp. 5815 - 5824.

Reference # 3 : an (almost) optimal synthesis method
A. De Vos and Y. Van Rentergem published an almost optimal synthesis method for an arbitrary reversible circuit, based on dual Young subgroups and the Birkhoff theorem on doubly stochastic matrices : `` Young subgroups for reversible computers '', in the journal Advances in Mathematics of Communications, volume 2 (2008), pp. 183 - 200.

Reference # 4 : a survey on chip performance
S. Burignat and A. De Vos published `` A review on the performance of reversible ripple-adders '', in the International Journal of Electronics and Telecommunications, volume 58 (2012), pp. 205 - 212.

Reference # 5 : a first step towards quantum computing
A. De Vos, J. De Beule and L. Storme published a paper on the quantum gate known as the square root of NOT: `` Computing with the square root of NOT '', in the Serdica Journal of Computing, volume 3 (2009), pp. 359 - 370.

Reference # 6 : a large step into the quantum world
A. De Vos and S. De Baerdemacker have published a paper on the quantum gate known as the NEGATOR: `` The NEGATOR as a basic building block in quantum circuits '', in the journal Open Systems and Information Dynamics, volume 20 (2013), p. 1350004.

Reference # 7 : a challenging conjecture
In January 2014, A. De Vos and S. De Baerdemacker have put forward a conjecture about unitary matrices: `` Scaling a unitary matrix '', in the arXiv, published in the journal Open Systems and Information Dynamics, volume 21 (2014), p. 1450013. In August 2014, the conjecture was proved by Idel and Wolf, in the arXiv.

Reference # 8 : a quantum synthesis method
A. De Vos and S. De Baerdemacker have published a paper, on quantum computers: `` Block-ZXZ synthesis of an arbitrary quantum circuit '', in the journal Physical Review A, volume 94 (2016), p. 052317.

Reference # 9 : a mathematical theorem
S. De Baerdemacker, A. De Vos, L. Chen, and L. Yu have published a first paper, a second paper, a third paper, and a fourth paper on a unitary version of Birkhoff's theorem, in the journal Linear Algebra and its Applications, volume 493 (2016), pp. 455 - 468, volume 514 (2017), pp. 151 - 164, volume 578 (2019), pp. 27 - 52, and volume 606 (2020), pp. 23 - 40.

Reference # 10 : an endoreverible model
A. De Vos has published paper on endoreversible modelling of computing, in the special issue on finite-time thermodynamics of the journal Entropy, volume 22 (2020), p. 660.

AND PLEASE READ THIS ONE :

In its March-April 2006 issue (pp. 107-111), the journal American Scientist

has published a review paper entitled `Reverse engineering',
with a photograph of one of our circuits !

AND PLEASE READ THE TEXTBOOKS :


Wiley-VCH, Springer Verlag, and Morgan & Claypool have published
the following textbooks on reversible computing:
`Reversible computing' (251 pages),
`Towards a design flow for reversible logic' (184 pages), and
`Synthesis of quantum circuits versus synthesis of classical reversible circuits' (125 pages):




AND, FINALLY, PLEASE VIEW THE MOVIE :


Since February 2014, an 8-minutes movie about the bilateral research project MicroPower (see below) is available in three versions (each 552 MegaBytes):
a version without subtitles (partly in English and partly in Dutch),
a version with English subtitles, and
a version with Danish subtitles.
The movie was produced in a collaboration between Københavns Universitet, the Universiteit Gent, and the company fisheye.


This page
http://www.elis.UGent.be/~aldevos/projects/computer.html
is maintained by Alexis De Vos
(alexis.devos@ugent.be).
Last maintenance on 28 September 2021.