|
SPRAAK
|
|
SPRAAK
|
This section deal with a modification to SPRAAK in order to improve its robustness to noise and possibly reverberation. It does NOT improve robustness to pronunciation variation or accents. It is based on MISSING DATA THEORY (MDT). The principles of the approach are explained below. As a user, you need to be aware of the following:
This implementation is largely based on [1]. At each frame 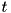 , the log of the speech power spectrum is represented by a vector
, the log of the speech power spectrum is represented by a vector  . If the data are perturbed by noise, this spectral vector becomes
. If the data are perturbed by noise, this spectral vector becomes 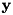 . In absence of speech, the spectral vector would be
. In absence of speech, the spectral vector would be 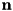 (only due to noise). Next to the spectral data, a mask
(only due to noise). Next to the spectral data, a mask  is also estimated. For now, it is assumed it is a binary vector, with
is also estimated. For now, it is assumed it is a binary vector, with 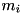 =1 meaning the spectral value
=1 meaning the spectral value 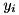 being unreliable and a 0 meaning it is reliable. The reliable data is just copied from the noisy input, i.e.
being unreliable and a 0 meaning it is reliable. The reliable data is just copied from the noisy input, i.e. 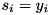 if
if 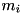 =0. The unreliable data will be reconstructed or imputed based on the clean speech model. (Notice that there is also an MDT method in which it is marginalized out.) In the SPRAAK implementation, this imputation is guided by the search process, i.e. the missing data is reconstructed for each assumption the back-end makes about the speech identity. In this context, assumption means the visited state and selected Gaussian from its mixture. The missing data is reconstructed based on the maximum likelihood principle, i.e. it looks for the most likely values of the unreliable spectral components. The negative log-likelihood of a Gaussian model is a quadratic (within a constant):
=0. The unreliable data will be reconstructed or imputed based on the clean speech model. (Notice that there is also an MDT method in which it is marginalized out.) In the SPRAAK implementation, this imputation is guided by the search process, i.e. the missing data is reconstructed for each assumption the back-end makes about the speech identity. In this context, assumption means the visited state and selected Gaussian from its mixture. The missing data is reconstructed based on the maximum likelihood principle, i.e. it looks for the most likely values of the unreliable spectral components. The negative log-likelihood of a Gaussian model is a quadratic (within a constant):
![\[ L(\mathbf{s}) = (\mathbf{s} - \mathbf{\mu} )^T \mathbf{\Sigma}^{-1} (\mathbf{s} - \mathbf{\mu} ) \hspace{3cm}(1)\]](form_10.png)
which is to be minimized over the unreliable components of  . However, there are useful constraints that can be imposed on
. However, there are useful constraints that can be imposed on  . Though this is an approximation neglecting the phase relations between the spectra, MDT assumes:
. Though this is an approximation neglecting the phase relations between the spectra, MDT assumes:
![\[\mathbf{s} \leq \mathbf{y} \hspace{4.5cm}(2)\]](form_11.png)
Hence, (1) is to be minimized over the unreliable components of  under constraint (2), and this for every Gaussian and for every frame. Notice that in (1),
under constraint (2), and this for every Gaussian and for every frame. Notice that in (1), 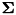 is not a diagonal matrix, since
is not a diagonal matrix, since  is a vector of log-spectra and not cepstra (or any diagonalizing transform). In SPRAAK, the constrained optimization (1)+(2) is solved with a gradient descent method, which is computationally efficient and requires only a few iterations to converge to a sufficiently accurate solution (controled by the parameter 'MDTiter=<nr>;' in the MDT options string; the default value is 2; 0 means trivial spectral imputation only).
is a vector of log-spectra and not cepstra (or any diagonalizing transform). In SPRAAK, the constrained optimization (1)+(2) is solved with a gradient descent method, which is computationally efficient and requires only a few iterations to converge to a sufficiently accurate solution (controled by the parameter 'MDTiter=<nr>;' in the MDT options string; the default value is 2; 0 means trivial spectral imputation only).
For the delta (derivative) features, the likelihood maximization (1) remains valid, but the constraints (2) need to be changed. Due to the noise, the clean value of the delta feature can be both greater than or less than the noisy value. Therefore, a ternary mask is used:
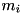 =0 means
=0 means 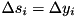
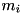 =1 means
=1 means 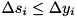
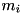 =2 means
=2 means 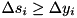
The benefit of applying MDT to delta's is questionable in that on some data sets, no improvement was observed. To disable MDT for delta's, simply generate an all-zero mask.
A non-MDT model would evaluate the Gaussians at the noisy data (after applying a diagonalizing transform). In MDT with Gaussian-based imputation, the evaluation of a likelihood is replaced by non-negative least squares (NNLSQ) problem (1)+(2). The solution of the NNLSQ problem requires an order of magnitude more computational effort than evaluating a Gaussian with diagonal covariance. Indeed, the last is linear in the feature vector dimension, while the former is quadratic or even cubic and requires iteration.
A first optimization that is performed is to use a different feature set. In [2], it is shown that the NNLSQ problem can be solved with significantly less effort if the log-spectra are (linearly) transformed to the ProSpect representation, while there is no impact on accuracy.
To cut computational costs, a multi candidate approach was designed. The idea is to constrain  to a discrete set of values generated by solving the NNLSQ problem on a set of cluster Gaussians. This has several advantages:
to a discrete set of values generated by solving the NNLSQ problem on a set of cluster Gaussians. This has several advantages:
The multi candidate approach requires an association table. For each backend Gaussian, it lists which are the cluster Gaussians that have yielded the best candidates  on training data.
on training data.
The MDT implementation then works as follows: all the (ProSpect) cluster Gaussians are evaluated on the current frame using MDT. Only the cluster Gaussians with the highest likelihood are maintained (the L-cluster-M-best method of [3] or [4]). Each of these cluster Gaussians generates an imputed speech estimate. The likelihood of a each backend Gaussian is then given by its likelihood evaluated at the candidate yielding the highest likelihood among the candidates listed in the association table for that Gaussian. Typically 3 to 10 candidates are considered.
Linear filtering (different microphones, bandwidth limitations, ...) have a detrimental effect on ASR. In a non-MDT recognizer, a commonly used approach is cepstral mean normalization in which the mean of the cepstral vector is subtracted from the inputs. Equivalently, the mean of the log-spectrum can be subtracted from the log-spectral features. In MDT, this does not make much sense, since part of the data are assumed to be unreliable. Therefore, in SPRAAK, the channel estimate is a maximum likelihood estimate, i.e. the log-spectral vector that maximizes the likelihood of the feature stream under the backend model. The channel estimate should also be applied to the cluster Gaussians and to any speech model that is used in the mask estimator. This is for instance the case in the VQ-based mask estimator. The ML estimate is computed via iterative optimization and needs initialization. It is suggested to initialize it from a log-spectral mean estimate, computed in the preprocessing script. During recognition, the likelihood of the data is maximized by modifying the channel estimate (an offset vector on the data or equivalently on the Gaussian means) along the Viterbi backtrace path (without modifying the path). The channel update happens only on the common part of all backtraces from feasible active states. (When the end of the utterance is reached, there is only one feasible state, so all data will be processed eventually.) Both initialization and update strategy imply that, like in CMN, a sufficient amount of speech data must be processed before the channel estimate is reliable. Therefore, the accuracy may be improved by repeatedly processing the same utterance after a channel change, if the evaluation restrictions allow this.
[1] Maarten Van Segbroeck and Hugo Van hamme. Advances in Missing Feature Techniques for Robust Large Vocabulary Continuous Speech Recognition. IEEE Transactions on Audio, Speech and Language Processing, volume 19, No. 1, pages 123-137, January 2011.
[2] Hugo Van hamme. PROSPECT Features and their Application to Missing Data Techniques for Robust Speech Recognition. In Proc. International Conference on Spoken Language Processing, volume I, pages 101–104, Jeju Island, Korea, October 2004.
[3] Yujun Wang, Maarten Van Segbroeck and Hugo Van hamme. Robust Large Vocabulary Continuous Speech Recognition Based on Missing Feature Techniques. In J. Ramírez and J.M. Górriz, editors, Recent Advances in Robust Speech Recognition Technology, pages 141-154, Bentham Science Publishers. 2011. eISBN 978-1-60805-172-4.
[4] Wang Yujun and Hugo Van hamme. Speed improvements in a Missing Data-based speech recognizer. In Proceeding of NAG-DAGA2009, Rotterdam, Netherlands, april 2009.
 1.8.6
1.8.6